论文分享——弹性聚合方法应用于联邦学习
论文链接:https://ieeexplore.ieee.org/document/10204999
发表会议:CVPR 2023
1 摘要
众所周知,联邦学习面临数据异构时可能会出现训练结果不稳定以及收敛速度变慢的问题。这篇文章主要提出了一种新的聚合方法——弹性聚合来克服这些问题,根据参数灵敏度来自适应的插入客户端模型。
2 引言
联邦学习是一种隐私保护的分布式学习框架,它允许每个本地客户端训练一个由中央服务器分发的全局模型,服务器再聚合所有参与训练的设备的模型参数以获得一个新的全局模型。联邦学习的出现,解决了数据隐私和数据孤岛的问题。联邦学习具有以下四个关键特征:
(1)不可靠的链接:连接服务器和客户端的链接可能不可靠,并且在任何给定时间只有很小一部分客户端可能处于活动状态
(2)大规模分布:客户端数量通常很多,但每个客户端的数据量相对较小
(3)客户端间的异构:客户端数据是异构且非独立同分布的,意味着来自不同客户端的数据可以从采样空间的不同区域中抽样
(4)数据的不平衡:每个客户端可用的数据量可能存在显著的不平衡
传统的联邦学习聚合算法例如FedAvg,在客户端上执行多轮本地更新,发送给服务器进行参数的聚合。也就是说,在局部数据上训练最小化经验损失函数似乎在同构场景下表现良好;但是,这样做与全局最小化经验损失函数从根本上是不一致的。客户端的更新可能会使服务器模型偏离了理想的分布,这种现象被称为“client drift”。
在这篇文章中,提出了一种弹性聚合的方法来解决“client drift”现象。使用未标记的客户端样本来测量参数的灵敏度,在客户端模型聚合期间,减少对敏感参数的更新,以防止服务器模型漂移到某一客户端的数据分布。相反,提高不太敏感参数的更新,可以更好地探索不同的客户端数据分布。
本文贡献:
(1)弹性聚合使用参数敏感性的概念来解决跨客户机数据的分布不一致问题,并且易于实现,几乎不需要超参数调优。
(2)参数灵敏度以在线和无监督的方式计算,从而更好地利用客户端在运行时生成的未标记数据。
(3)真实数据表明,弹性聚合方法在四种联邦学习场景下都可以得到有效地训练。
3 研究方法
文章的主要思想就是,不太敏感的参数可以自由更新,以尽量减少单个客户端的损失,而不会导致服务器模型漂移到某一客户端;通过同样的推理,更敏感的参数不应该更新那么多。如下图所示:
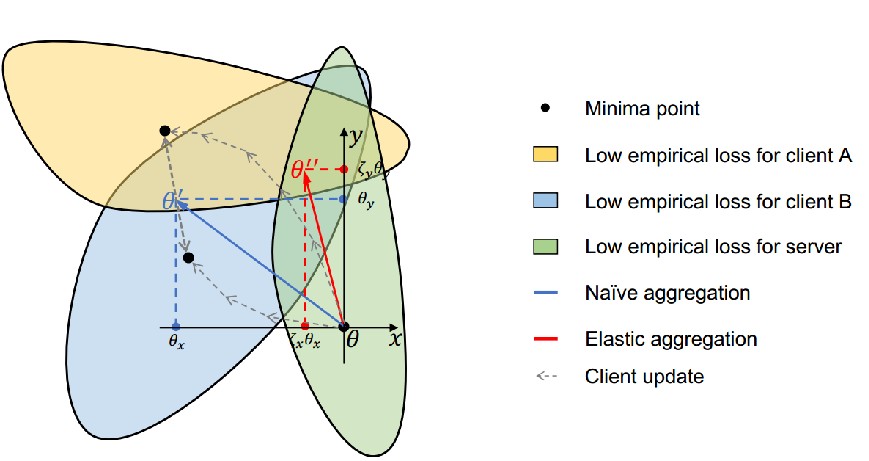 下面是方法的伪代码:
下面是方法的伪代码:

3.1 参数灵敏度的测量
通过梯度g(θ^i;x)即对参数的小扰动判断对模型输出的影响来测量参数灵敏度Ωi:
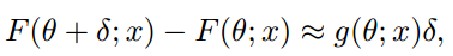
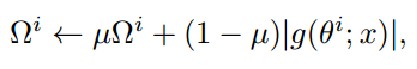
3.2 弹性聚合
通过上一步可以得到参数的灵敏度Ωi,根据Ωi计算灵敏度自适应系数:
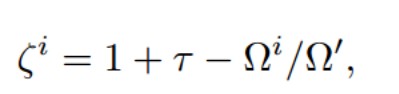 然后,进行服务器端的弹性聚合:
然后,进行服务器端的弹性聚合:
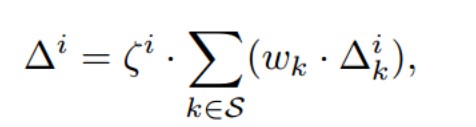 使用灵敏度自适应系数对参数进行加权,来实现减少对敏感参数的更新,降低对不敏感参数的更新程度。
使用灵敏度自适应系数对参数进行加权,来实现减少对敏感参数的更新,降低对不敏感参数的更新程度。
以上就是本文提出的方法
4 实验结果
大家可以去原文处看看实验结果,总结来说就是在数据集异构程度较高的情况下能得到比传统聚合算法(FedAvg Fedprox FedAvgM)更好的结果(说了好像没说,没太仔细看/////////)
5 总结与展望
本文提出了弹性聚合的联邦学习算法,利用参数敏感性克服梯度不相似性,克服异构场景下的精度不稳定、收敛慢的问题。方法思想其实看着挺简单的,但是会导致额外的计算负担和通信成本,考虑更实际的应用场景,这些问题也是需要克服的。
- 发表于 2024-02-23 17:30
- 阅读 ( 2578 )
