论文链接：https://arxiv.org/pdf/2202.05594.pdf

发表会议：IJCAI 2022

摘要

在过去的几年里，Shapley值，一个来自合作博弈论的解决方案概念，在机器学习中得到了大量的应用。本文首先讨论了合作博弈论的基本概念和Shapley值的公理化性质。然后，我们概述了Shapley值在机器学习中最重要的应用:特征选择、可解释性、多智能体强化学习、集成修剪和数据估值。我们研究了Shapley值的最关键的局限性，并指出了未来研究的方向。

引言

测量重要性和各种收益的归属是机器学习许多实际方面的核心问题，如可解释性，特征选择，数据估值，集成修剪和联邦学习。例如，有人可能会问:在机器学习模型的决策中，一个特征的重要性是什么?单个数据点值多少钱?在集合中哪些模型最有价值?这些问题已经在不同的领域使用特定的方法得到了解决。有趣的是，作为可转移效用(TU)合作博弈的解决方案，这些问题也有一种通用和统一的方法。与其他方法相比，TU对策的解概念在理论上具有公理化性质。最著名的解决方案是Shapley值，其特征是包括公平性、对称性和效率。

在TU设置中，一个合作博弈包括:一个参与者集和一个定义联盟(参与者子集)值的标量值特征函数。在这样的博弈中，Shapley值提供了一种严格而直观的方式来分配团队的集体价值(例如收入、利润或成本)。

为了将这一思想应用到机器学习中，我们需要定义两个组件:玩家集和特征函数。在机器学习环境中，玩家可能由一组输入特征、强化学习智能体、数据点、集合中的模型或数据筒仓来表示。然后，特征函数可以描述模型的拟合优度，奖励强化学习，实例级预测的财务收益，或样本外模型性能。我们在图1中提供了一个关于集合中模型估值的例子。

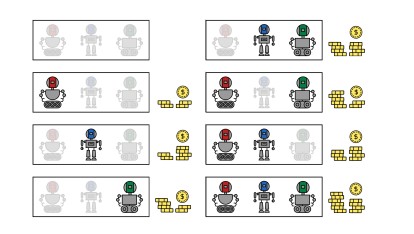
图1:Shapley值可以用于解决合作博弈。

集合中的模型是玩家(红色、蓝色和绿色机器人)，预测的经济收益是每个可能的联盟(矩形)的回报(硬币)。Shapley值可以在模型之间分配大联盟的收益(右下角)。

我们介绍了合作博弈的基本定义，并提出了Shapley值，这是一个可以将这些博弈中的收益分配给单个玩家的解决方案概念。我们将讨论它的属性，并强调为什么这些属性在机器学习中很重要。我们概述了Shapley值在机器学习中的应用:特征选择、数据估值、可解释性、强化学习和模型估值。最后，我们讨论了Shapley值的局限性，并指出了未来的发展方向。

背景

本节介绍合作博弈和Shapley值及其性质。我们还为我们的定义提供了一个说明性的运行示例。

合作博弈与Shapley值

定义1。玩家设置和联盟。设N ={1，…， n}是有限参与人的集合。我们称每个非空子集S⊆N为联盟，N本身为大联盟。

定义2。合作博弈。TU博弈由(N, v)对定义，其中v: 2N→R是一个称为博弈的特征函数或联盟函数，为每个联盟分配一个实数，并满足v(∅)= 0。

例1。让我们考虑一个3人合作博弈，其中N ={1,2,3}。特征函数定义了每个联盟的收益。让这些收益为:

定义3。可行收益向量的集合。定义合作博弈(N, v)的可行收益向量集合Z(N, v) = {Z∈RN | pi∈nzi≤v(N)}。

定义4。解的概念和解向量。解概念Φ是一个将子集Φ(N, v)⊆Z(N, v)关联到每个TU博弈(N, v)的映射。如果Φ(N, v)∈Φ(N, v)，则解向量Φ(N, v)∈RN到合作博弈(N, v)满足解概念Φ。如果对于每个(N, v)集合Φ(N, v)是单值的，则解概念Φ是单值的。

解决方案概念定义了分配原则，通过该原则可以将奖励分配给单个玩家。这些奖励的总和不能超过大联盟v(N)的价值。解向量是满足解概念原理的特定分配。

定义5。玩家设置的排列。设Π(N)是定义在N上的所有排列的集合，一个特定的排列记为Π∈Π(N)， Π(i)是参与人i∈N在排列Π中的位置

定义6。前任集。设参与人i∈N在排列π中的前集合为π πi = {j∈N | π(j) < π(i)}的联合。

让我们假设在我们的图解博弈中参与者的排列是π =(3,2,1)。在这种排列下，第一个参与者的前一集是π1 ={3,2}，第二个参与者的前一集是π2 = {3}， Pπ3 =∅。

定义7。Shapley值。Shapley值[Shapley, 1953]是合作博弈的单值解概念。对于任意合作对策(N, v)，满足此解概念的单解向量的第i分量由式给出。

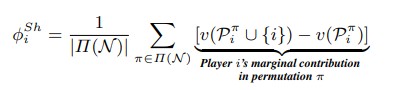
玩家的Shapley值是玩家对前一个集合的价值的平均边际贡献除以玩家集合的每一种可能的排列。

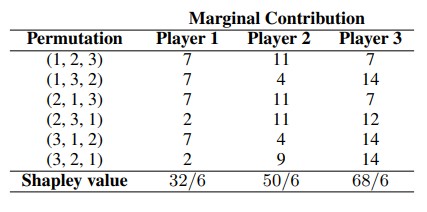
表1包含人工计算参与者对每个排列的边际贡献和例1中的Shapley值。

Shapley值的性质

近似的shapley值

Shapley值计算需要阶乘数的特征函数计算，造成阶乘时间复杂度。这在机器学习环境中是禁止的，因为每个评估都对应于训练一个机器学习模型。出于这个原因，机器学习应用程序使用了我们在本节中讨论的各种Shapley值逼近方法。

蒙特卡罗排列抽样

蒙特卡洛置换抽样是卡斯特罗等人首次提出的，用于在线性时间内近似Shapley值。他们的方法执行基于抽样的近似，在每次迭代中，从玩家集合的排列中抽取一个随机元素。参与者在抽样排列中的边际贡献按样本数量缩小(这相当于取平均值)，并添加到先前迭代的近似Shapley值中。Castro等人在边际贡献方差已知的情况下，通过中心极限定理为这种近似算法提供了渐近误差边界。Maleki等人扩展了这种抽样方法的分析，当方差或边际贡献的范围通过Chebyshev 's和Hoeffding 's不等式已知时，提供了误差界限。与之前的渐近边界相比，它们的边界适用于有限数量的样本。

除了扩展蒙特卡罗估计的分析之外，Maleki等人演示了如何通过将玩家集的排列划分为同质、不重叠的子种群来分层抽样，从而改进Shapley值近似。特别是，他们表明，如果一组排列可以划分为具有相似边际收益的玩家层，那么近似将更加精确。在此之后，Castro等人探索了分层抽样方法，当玩家处于联盟内的特定位置时，使用由所有边际贡献集定义的地层。Burgess等人提出了分层抽样方法，旨在通过分层经验伯恩斯坦界最小化估计的不确定性。

遵循Maleki等人的分层方法的其他方差减小技术卡斯特罗等人;Burgess等， Illés等人提出了样本均值的另一种方差缩减技术。它们不是生成随机样本序列，而是生成遍历但不独立的样本序列，利用负相关来减小样本方差。Mitchell等人[2021]表明，其他蒙特卡罗方差缩减技术也可以应用于这个问题，例如对偶抽样。一种简单形式的对偶抽样同时使用随机抽样排列和它的反向排列。最后，Touati等人引入了一种贝叶斯蒙特卡罗方法来计算Shapley值，表明使用贝叶斯方法可以改进Shapley值估计。

多线性扩展

通过在子集S上引入一个概率分布，其中Ei是一个不包括参与者i的随机子集，每个参与者都包含在一个概率为q的子集中。

因此，对q进行采样提供了一种近似方法——多线性扩展。例如，Mitchell等人使用梯形规则以固定间隔对q进行采样，而Okhrati等人[2021]提出将对偶采样作为方差减少技术。

线性回归逼近

在他们的重要工作中，Lundberg等人将Shapley值应用于特征的重要性和可解释性，证明TU博弈的Shapley值可以通过解决加权最小二乘优化问题来近似。他们的主要见解是通过近似解决以下优化问题来计算Shapley值:

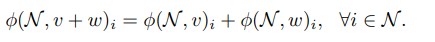
为了解决这一问题，Lundberg等人提出通过对联盟进行子抽样来逼近这一问题。注意，当联盟大或小时，wS会更高。Covert等人扩展了对该方法的研究，发现虽然SHAP是一个一致估计量，但它不是一个无偏估计量。通过提出并分析这种无偏方法的一种变化，他们得出结论，虽然SHAP产生了一个小偏差，但它的方差明显低于相应的无偏估计量。

机器学习和shapley值

我们在表2中总结了最重要的应用领域，并根据解决的问题对相关工作进行了分组。

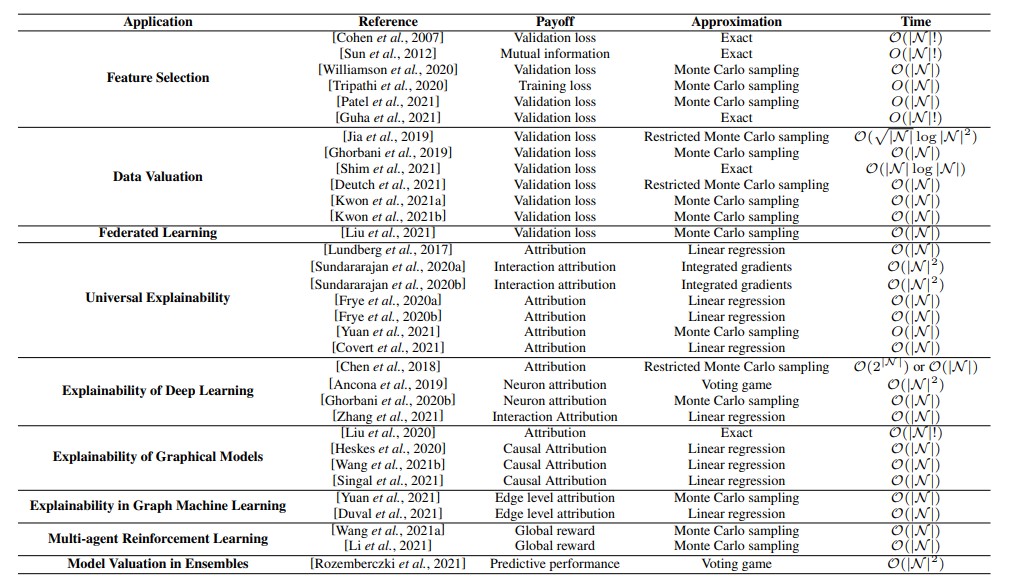
特征选择

联邦学习和强化学习

总结与展望